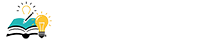先求出A的逆矩阵 A^(-1),然后再原式右乘 A的逆矩阵。
即XA=B那么X*A*A^(-1)=B*A^(-1)那么X*[A*A^(-1)]=B*A^(-1)那么X*E=B*A^(-1)即X=B*A^(-1)定理(1)逆矩阵的唯一性。若矩阵A是可逆的,则A的逆矩阵是唯一的,并记作A的逆矩阵为A-1。
(2)n阶方阵A可逆的充分必要条件是r(A)=m。对n阶方阵A,若r(A)=n,则称A为满秩矩阵或非奇异矩阵。
(3)任何一个满秩矩阵都能通过有限次初等行变换化为单位矩阵。推论 满秩矩阵A的逆矩阵A可以表示成有限个初等矩阵的乘积。